HASHMAP

• Intro(HashMap) #

  hello hashmap

  • 构造器 #

    public HashMap(int initialCapacity, float loadFactor) {
        if (initialCapacity < 0)
            throw new IllegalArgumentException("Illegal initial capacity: " +
                                            initialCapacity);
        if (initialCapacity > MAXIMUM_CAPACITY)
            initialCapacity = MAXIMUM_CAPACITY;
        if (loadFactor <= 0 || Float.isNaN(loadFactor))
            throw new IllegalArgumentException("Illegal load factor: " +
                                            loadFactor);
        this.loadFactor = loadFactor;
        this.threshold = tableSizeFor(initialCapacity);
    }
    
    /**
     * Constructs an empty <tt>HashMap</tt> with the specified initial
     * capacity and the default load factor (0.75).
     *
     * @param  initialCapacity the initial capacity.
     * @throws IllegalArgumentException if the initial capacity is negative.
     */
    public HashMap(int initialCapacity) {
        this(initialCapacity, DEFAULT_LOAD_FACTOR);
    }
    
    /**
     * Constructs an empty <tt>HashMap</tt> with the default initial capacity
     * (16) and the default load factor (0.75).
     */
    public HashMap() {
        this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
    }
    

  • 初始容量 #

    实际是求取一个整形数值的最接近 \({\color{red}2^{n}}\) 的值。
    
    可以通过以下方法获取：
    \(2^{0} < x <= 2^{1}-1\) \(\hspace{5em} [00000000\quad00000000\quad00000000\quad0000000{\color{red}1}] - [00000000\quad00000000\quad00000000\quad0000000{\color{red}1}]\)
    \(2^{1} < x <= 2^{2}-1\) \(\hspace{5em} [00000000\quad00000000\quad00000000\quad000000{\color{red}10}] - [00000000\quad00000000\quad00000000\quad000000{\color{red}11}]\)
    \(2^{2} < x <= 2^{3}-1\) \(\hspace{5em} [00000000\quad00000000\quad00000000\quad00000{\color{red}100}] - [00000000\quad00000000\quad00000000\quad00000{\color{red}111}]\)
    \(2^{3} < x <= 2^{4}-1\) \(\hspace{5em} [00000000\quad00000000\quad00000000\quad0000{\color{red}1000}] - [00000000\quad00000000\quad00000000\quad0000{\color{red}1111}]\)
    \(2^{4} < x <= 2^{5}-1\) \(\hspace{5em} [00000000\quad00000000\quad00000000\quad000{\color{red}10000}] - [00000000\quad00000000\quad00000000\quad000{\color{red}11111}]\)
    \(\hspace{2.5em}\vdots\)
    \(2^{28} < x <= 2^{29}-1\) \(\hspace{4.3em} [000{\color{red}10000\quad00000000\quad00000000\quad00000000}] - [000{\color{red}11111\quad11111111\quad11111111\quad11111111}]\)
    \(2^{29} < x <= 2^{30}-1\) \(\hspace{4.3em} [00{\color{red}100000\quad00000000\quad00000000\quad00000000}] - [00{\color{red}111111\quad11111111\quad11111111\quad11111111}]\)
    \(2^{30} < x <= 2^{31}-1\) \(\hspace{4.3em} [0{\color{red}1000000\quad00000000\quad00000000\quad00000000}] - [0{\color{red}1111111\quad11111111\quad11111111\quad11111111}]\)

    1). 由上述规律可知：若求取一个值的最接近的2次方，实际上是获取该数字的二进制最高位1，然后将最高位位置右边的值都设置为1，最后+1,即所需要的值。这个可以通过jdk1.7中扩容方法中调用的方法名: Integer.highestOneBit()猜验。
    例如10的二进制为 \([0000 {\color{red}1}010]\) ,则最高位1在第四位，第四位右边的都为1后二进制为 \([0000 {\color{red}1111}]\) , 最后+1即 \([000{\color{red}10000}]\) = 16。
    
    2). 至于为什么刚开始就-1。则是因为如果一个值本身就是所需要的值。例如对于16(\(2^4\))它需要的值为16,但是按照刚才的方法下来后取的值为32(\(2^5\)) 了就。
    而且-1操作对其他值没有影响。例如计算8 <–> 16 中的值。如果为8，则-1后为7,最后取值为8.如果为9，则-1为8，最后取值为16。
    
    3). 为什么只到n |= n >>> 16;,而没有n |= n >>> 32;？
    我们可以举例说明。因为最大值=MAXIMUM_CAPACITY = 1 << 30, 即 \([0{\color{red}1}000000\quad00000000\quad00000000\quad00000000]\)
    如果传入的值为\([0{\color{red}1}000000\quad00000000\quad00000000\quad00000001]\)。
    减一后 \([0{\color{red}1}000000\quad00000000\quad00000000\quad00000000]\) 。
    n |= n >>> 1; \(\hspace{1em}[0{\color{red}11}00000\quad00000000\quad00000000\quad00000000]\) 。
    n |= n >>> 2; \(\hspace{1em}[0{\color{red}1111}000\quad00000000\quad00000000\quad00000000]\) 。
    n |= n >>> 4; \(\hspace{1em}[0{\color{red}1111111\quad1}0000000\quad00000000\quad00000000]\) 。
    n |= n >>> 8; \(\hspace{1em}[0{\color{red}1111111\quad11111111\quad1}0000000\quad00000000]\) 。
    此时值在31-16位都已经为1了。所以对于一个整形int值，只需要在移动16位即可，移动32位没有任何意义。
    n |= n >>> 16; \(\hspace{0.5em}[0{\color{red}1111111\quad11111111\quad11111111\quad11111111}]\) 。
    则根据程序逻辑n >= MAXIMUM_CAPACITY,取值为MAXIMUM_CAPACITY = \(2^{30}\) 。

    static final int MAXIMUM_CAPACITY = 1 << 30;
    
    /**
     * jdk 1.7 hashmap 根据参数计算tablesize
     * @param number
     * @return
     */
    private static int roundUpToPowerOf2(int number) {
        // assert number >= 0 : "number must be non-negative";
        return number >= MAXIMUM_CAPACITY
                ? MAXIMUM_CAPACITY
                : (number > 1) ? Integer.highestOneBit((number - 1) << 1) : 1;
    }
    
    /**
     * jdk 1.8 hashmap 根据参数计算tablesize
     * @param cap
     * @return
     */
    static final int tableSizeFor(int cap) {
        int n = cap - 1;
        n |= n >>> 1;
        n |= n >>> 2;
        n |= n >>> 4;
        n |= n >>> 8;
        n |= n >>> 16;
        return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
    }
    

  • 扰动函数 #

    理论上散列值是一个int型，如果直接拿散列值作为下标访问HashMap主数组的话，考虑到2进制32位带符号的int表值范围从-2147483648到2147483648。前后加起来大概40亿的映射空间。只要哈希函数映射得比较均匀松散，一般应用是很难出现碰撞的。

    使用扰动函数的目的是让hashcode的高16位也参与散列运算。混合原始哈希码的高位和低位，以此来使低位的随机性更好。

    static final int hash(Object key) {
        int h;
        return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
    }
    

  • 计算下标 #

    通过(n - 1) & hash 代码计算table下标[n 为table的长度]。将通过扰动后的hash值与table长度 - 1的值进行&运算取得下标index。
    
    为什么会& (n - 1)?
    因为 n 为 \({\color{red}2^{n}}\) ,假如 n = 16 = \((2^{4})\) 。则 n - 1 = \([0000 1111]\)
    则将任何值与 \([0000 1111]\) 进行 & 运算都会得到 \([0000 0000] \sim [0000 1111]\) ，即 0 ~ 15，也就是table的下标值。这也是为什么table长度取 \({\color{red}2^{n}}\) 的原因。

  • 扩容方法 #

    • resize() #

      /**
       * Initializes or doubles table size.  If null, allocates in
       * accord with initial capacity target held in field threshold.
       * Otherwise, because we are using power-of-two expansion, the
       * elements from each bin must either stay at same index, or move
       * with a power of two offset in the new table.
       *
       * @return the table
       */
      final Node<K,V>[] resize() {
          Node<K,V>[] oldTab = table;
          int oldCap = (oldTab == null) ? 0 : oldTab.length;
          int oldThr = threshold;
          int newCap, newThr = 0;
          if (oldCap > 0) {
              if (oldCap >= MAXIMUM_CAPACITY) {
                  threshold = Integer.MAX_VALUE;
                  return oldTab;
              }
              else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                      oldCap >= DEFAULT_INITIAL_CAPACITY)
                  newThr = oldThr << 1; // double threshold
          }
          else if (oldThr > 0) // initial capacity was placed in threshold
              newCap = oldThr;
          else {               // zero initial threshold signifies using defaults
              newCap = DEFAULT_INITIAL_CAPACITY;
              newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
          }
          if (newThr == 0) {
              float ft = (float)newCap * loadFactor;
              newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                      (int)ft : Integer.MAX_VALUE);
          }
          threshold = newThr;
          @SuppressWarnings({"rawtypes","unchecked"})
              Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
          table = newTab;
          if (oldTab != null) {
              for (int j = 0; j < oldCap; ++j) {
                  Node<K,V> e;
                  if ((e = oldTab[j]) != null) {
                      oldTab[j] = null;
                      if (e.next == null)
                          newTab[e.hash & (newCap - 1)] = e;
                      else if (e instanceof TreeNode)
                          ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                      else { // preserve order
                          Node<K,V> loHead = null, loTail = null;
                          Node<K,V> hiHead = null, hiTail = null;
                          Node<K,V> next;
                          do {
                              next = e.next;
                              if ((e.hash & oldCap) == 0) {
                                  if (loTail == null)
                                      loHead = e;
                                  else
                                      loTail.next = e;
                                  loTail = e;
                              }
                              else {
                                  if (hiTail == null)
                                      hiHead = e;
                                  else
                                      hiTail.next = e;
                                  hiTail = e;
                              }
                          } while ((e = next) != null);
                          if (loTail != null) {
                              loTail.next = null;
                              newTab[j] = loHead;
                          }
                          if (hiTail != null) {
                              hiTail.next = null;
                              newTab[j + oldCap] = hiHead;
                          }
                      }
                  }
              }
          }
          return newTab;
      }
      

    • 需要注意的点 #

      

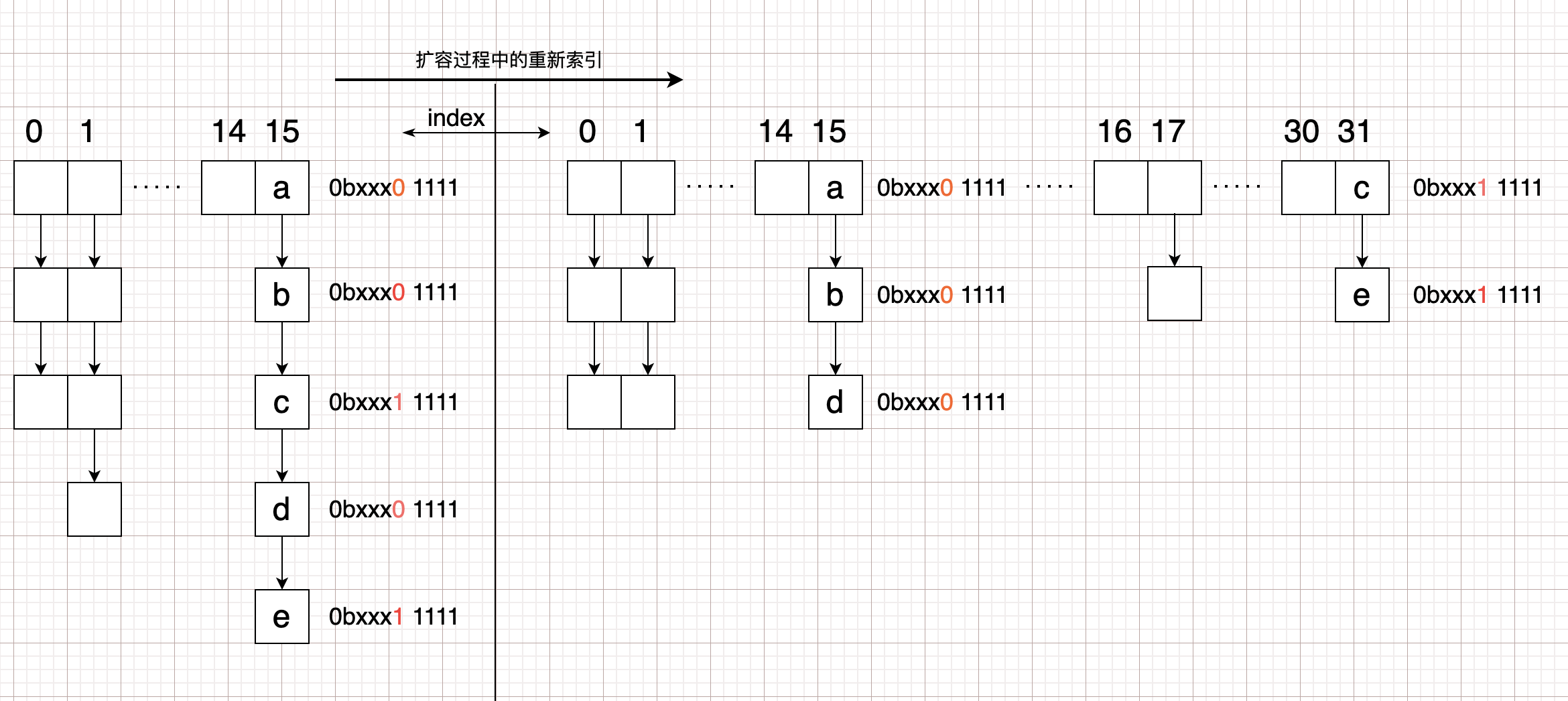
      1). 根据上图的规律可知。若数组长度大小固定，则可以推导出某个index的后半部分hash值。
      例如：若table.length=16。则在index=15的位置上。因为index = hash & (length -1 ),也即0b00001111 = hash & 1111。则hash值的后四位一定为1。
      若将a,b,c,d,e这些原在15位置上的hash值由原来的 \(16=2^4\) 重新分配到新数组 \(32=2^5\) 的时候，决定新下标的与值为11111。也就是原来15上面的0bxxx01111,还在15上(因为0bxxx01111 & 11111 = 15),而0bxxx11111,就分配在31了(因为0bxxx11111 & 11111 = 31)。
      
      2). 还有一个需要注意的点是resize()方法中的这 两行代码。翻译过来就是，如果当前下标中只有一个节点(单节点，不是链表，也不是红黑树)。为什么可以直接在新数组中使用newTab[e.hash & (newCap - 1)] = e;覆盖，难道不怕转移过程中存在hash冲突，有数据已经转移到新数组当前节点，而造成数据丢失吗？
      原因其实还可以用上方的图来解释：
      如果index=15的位置上只有一个节点a,则hash值肯定为0bxxxx1111。假设有其他节点会重新分配到新数组的话。则其他节点的hash后四位一定为1111。此时会存在矛盾，因为如果其他节点的hash后四位为1111的话，则原来一定存在15的位置上，不可能只有a元素一个。所以不用担心直接覆盖的情况，因为就只有一个。

  • NULL值问题 #

    // jdk 1.7 处理
    /**
     * 和hash值无关，put刚进来就会判断key==null。等于Null的话，直接往index=0的位置替换或头插。
     * addEntry() ==> createEntry(hash, key, value, bucketIndex);
     * createEntry():
     *      // 保存原来的链e
     *      Entry<K,V> e = table[bucketIndex];
     *      // 用刚才的值新建节点，并将next指向刚才保存的e。然后替换原来的链条，实现头插。
     *      table[bucketIndex] = new Entry<>(hash, key, value, e);
     */
    private V putForNullKey(V value) {
        for (Entry<K,V> e = table[0]; e != null; e = e.next) {
            if (e.key == null) {
                V oldValue = e.value;
                e.value = value;
                e.recordAccess(this);
                return oldValue;
            }
        }
        modCount++;
        addEntry(0, null, value, 0);
        return null;
    }
    
    // jdk 1.8 处理
    /**
     * 和hash值有关，Null值参与hash计算。得到的结果为0。
     * 经过下面的代码判断后发现存在null键值，后续会进行替换。
     */
    if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))
            e = p;
    ...
    
    if (e != null) { // existing mapping for key
        V oldValue = e.value;
        if (!onlyIfAbsent || oldValue == null)
            e.value = value; //替换存在的 null 值
        afterNodeAccess(e);
        return oldValue;
    }
    

  • 死链的形成(JDK1.7) #

    • put() #

      1). 头插
      2). 替换

      public V put(K key, V value) {
          if (table == EMPTY_TABLE) {
              inflateTable(threshold);
          }
          if (key == null)
              return putForNullKey(value);
          int hash = hash(key);
          int i = indexFor(hash, table.length);
          for (Entry<K,V> e = table[i]; e != null; e = e.next) {
              Object k;
              if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
                  V oldValue = e.value;
                  e.value = value;
                  e.recordAccess(this);
                  return oldValue;
              }
          }
      
          modCount++;
          addEntry(hash, key, value, i);
          return null;
      }
      

    • transfer() #

      /**
       * Transfers all entries from current table to newTable.
       */
      void transfer(Entry[] newTable, boolean rehash) {
          int newCapacity = newTable.length;
          for (Entry<K,V> e : table) {
              while(null != e) {
                  Entry<K,V> next = e.next;
                  if (rehash) {
                      e.hash = null == e.key ? 0 : hash(e.key);
                  }
                  int i = indexFor(e.hash, newCapacity);
                  e.next = newTable[i];
                  newTable[i] = e;
                  e = next;
              }
          }
      }
      

      1. 转换过程图

         转换过程就是，在index位置引用和它所指向的节点【NULL或者其他node】之间不断插入原来需要移动的节点。
         \(31 \to null\)
         \(31 \to a \to null\)
         \(31 \to b \to a \to null\)
         \(31 \to c \to b \to a -> null\)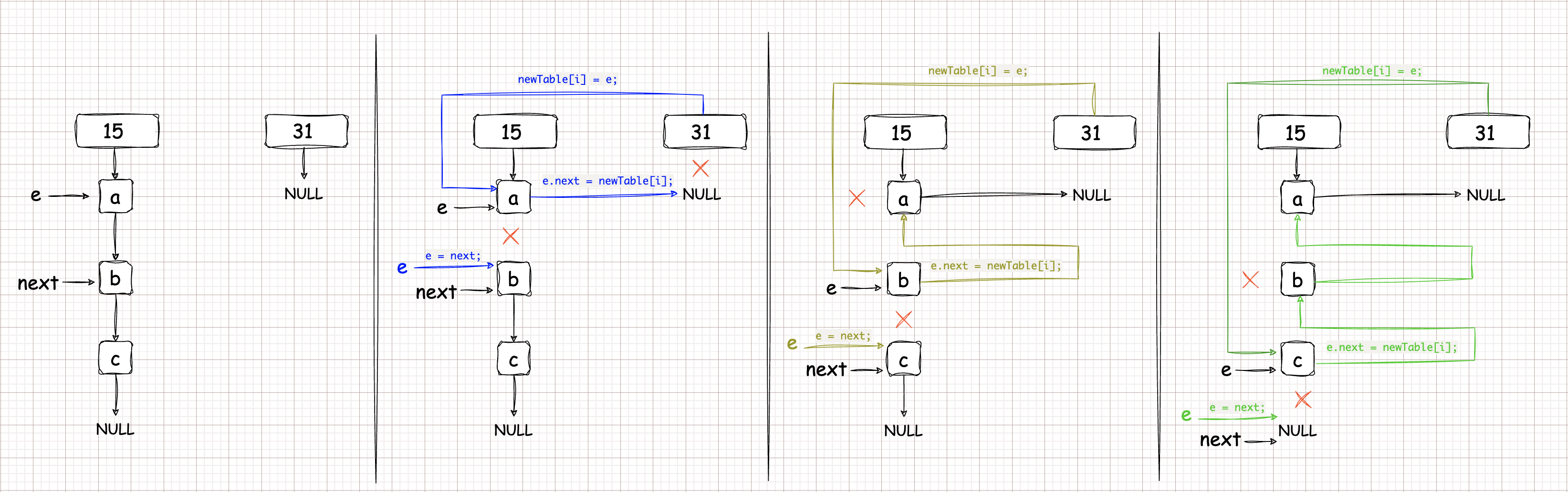

         

      2. 死链形成过程如下图

         假设线程1和线程2同时到达左边的状态。此时线程2挂起。完全由线程1进行transfer，完成后如右边所示。
         因为节点不管怎么移动。或者说节点之间怎么指向，都不会影响线程2中 \(e \to a ，e.next \to b\)。
         而线程2开始执行的时候发现，\(e \to a, e.next \to b\) 。结合 e, e.next 的语义可以发现：此时右边所示左右两个红框所表达的是一个意思也就是 \(a \to b\)。
         且由于线程1操作完成后 \(b \to a\) 的关系， 就造成死循环了。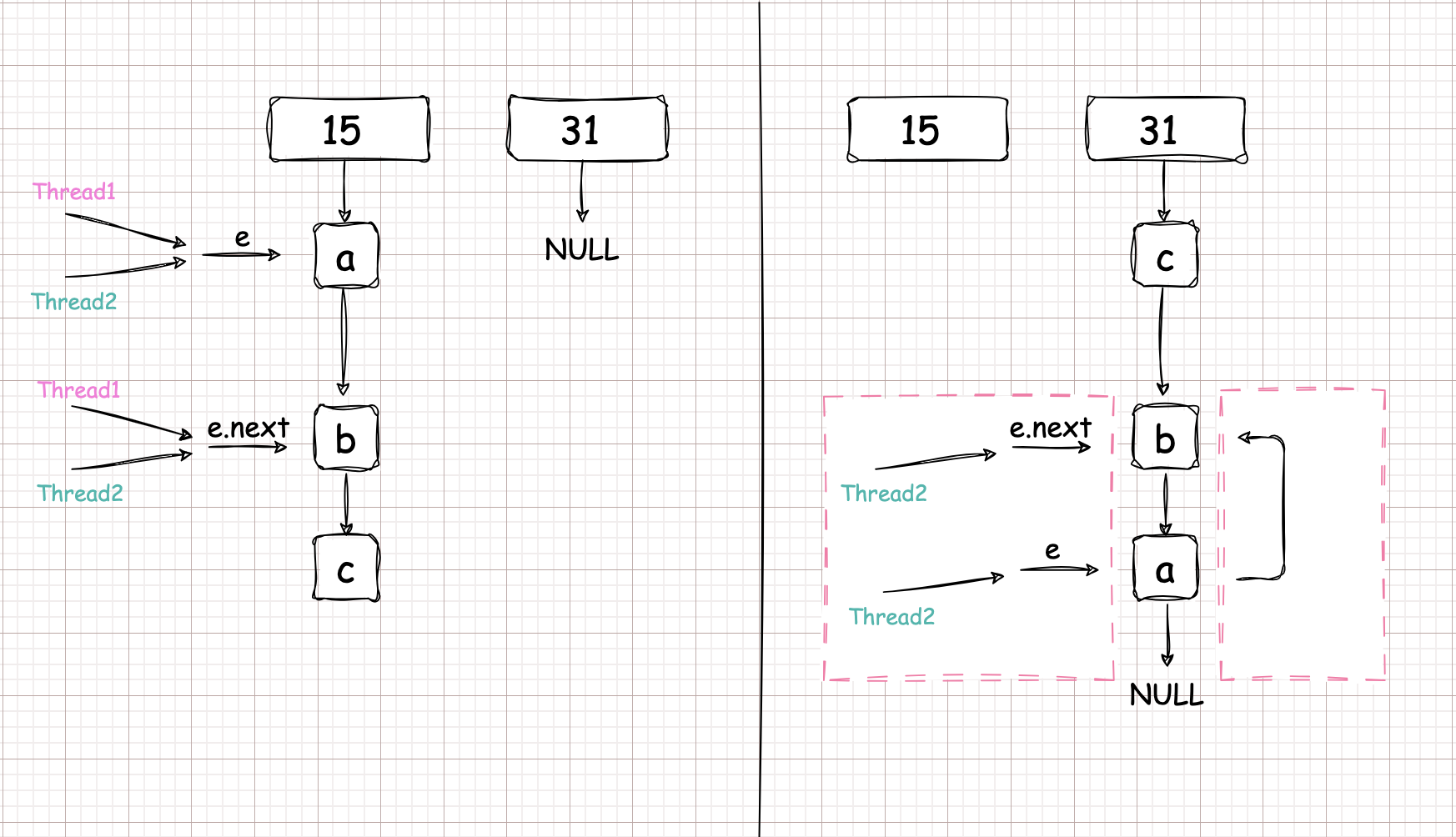

         

• Extends #

  • 解决哈希冲突的方法 #

    举例数列：[25, 18, 23, 3, 56, 87, 19, 37, 59]。

    • 开放定址法 #

      为产生冲突的地址 \(H(key)\)，按照某种规则产生另外一个地址的方法。

      1. 线性探测法

         \( H(key) = (H(key) + d) \hspace{0.4em} MOD \hspace{0.4em} m\);
         \(d = 1,2,3,4,5...n \)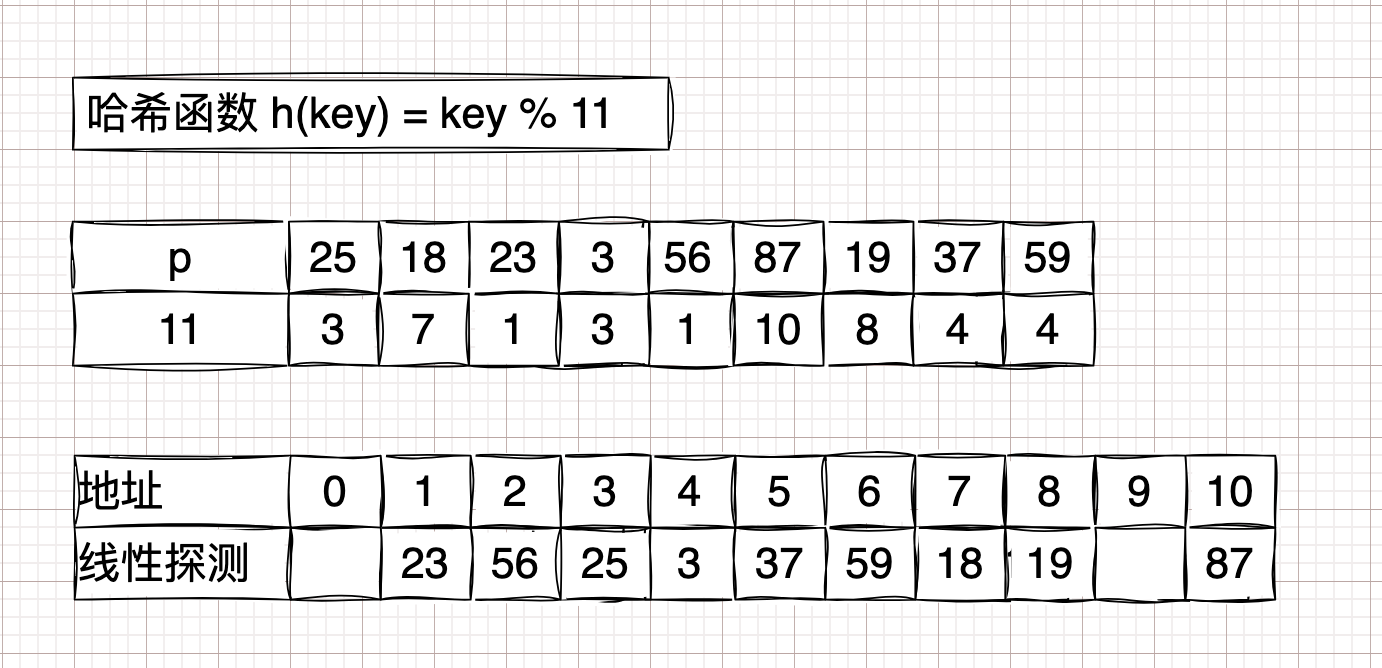

         

      2. 平方探测法

         \( H(key) = (H(key) + d) \hspace{0.4em} MOD \hspace{0.4em} m\);
         \(d = 1^2, -1^2, 2^2, -2^2, ... \)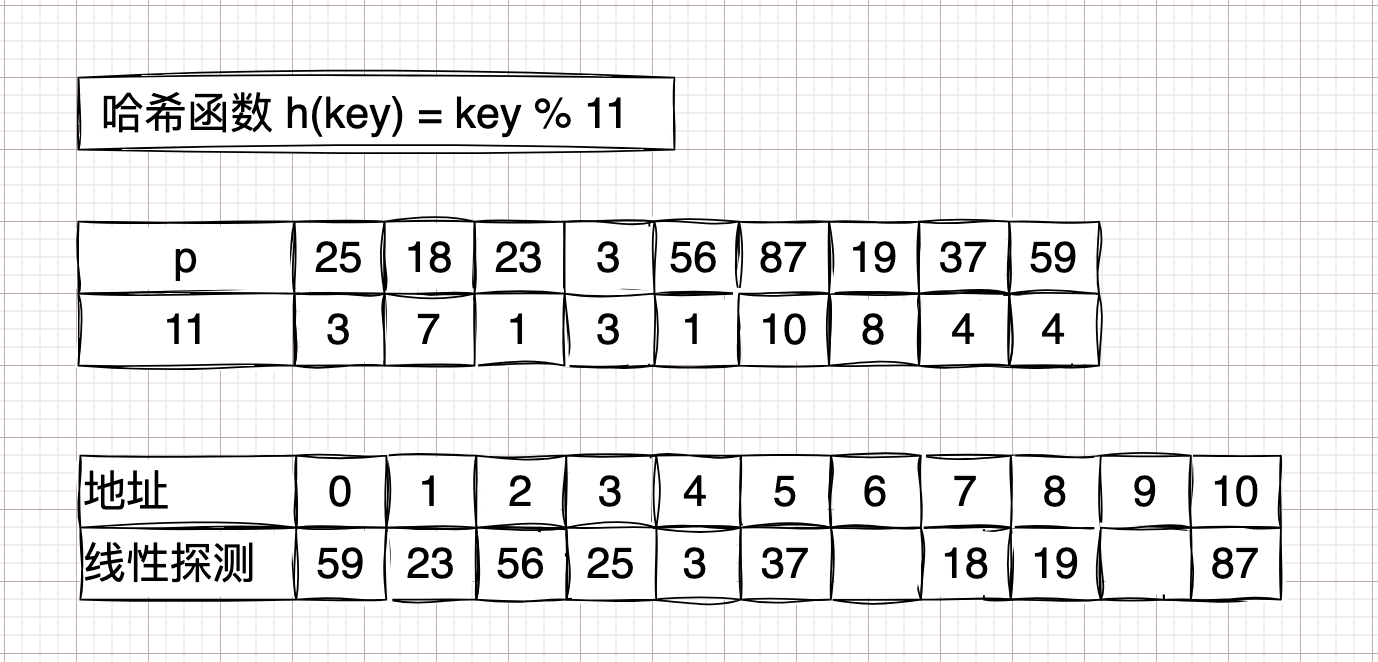

         

      3. 随机探测法

         \( H(key) = (H(key) + d) \hspace{0.4em} MOD \hspace{0.4em} m\);
         \(d = 3, 1, 9, 2, ... \) //一组伪随机数列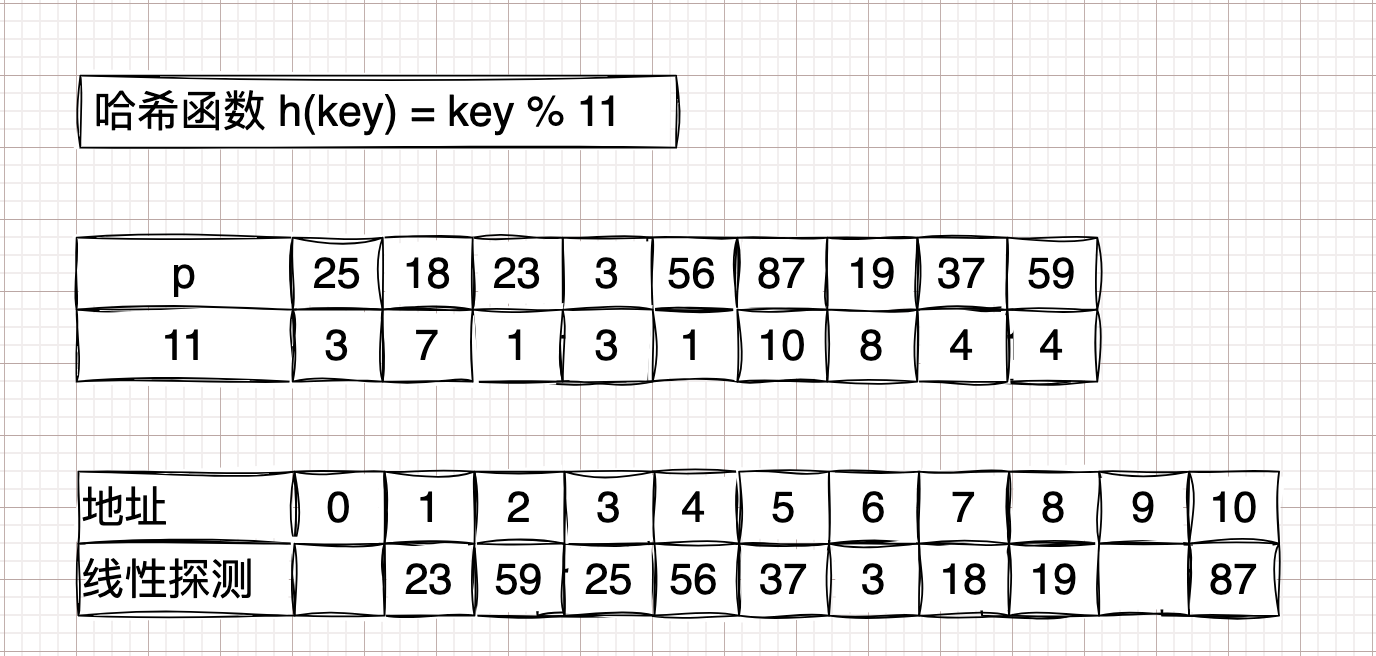

         

    • 链地址法(拉链法) #

      即hashmap中使用的方法，不再介绍。

    • 再哈希法 #

      这种方法是同时构造多个不同的哈希函数：\(H_d(key) = H_{d+1}(key), d = 1, 2, 3, ..., n \)
      当哈希地址 \(H(key)\) 发生冲突时，再计算\(H2(key)\)……，直到冲突不再产生。这种方法不易产生聚集，但增加了计算时间。

    • 建立公共溢出区 #

      散列表包含基本表和溢出表两个部分，将发生冲突的记录顺序存储到溢出表中。
      查找方法：通过 \(H(key)\) 函数计算散列地址，先在基本表中记录进行比较，若相等，则查找成功；否则，到溢出表中顺序查找。

      

• Problem #

  1. 解决哈希冲突的方法
  2. 扰动函数
  3. 空间大小，及扩容容量
  4. jdk1.7头插死链形成
  5. null值问题
  6. 字符串hashcode选31

• Reference #

  • https://www.bilibili.com/video/BV1b84y1G7o5
  • https://www.cnblogs.com/youzhibing/p/13915116.html
  • https://www.zhihu.com/question/20733617
  • https://drive.google.com/file/d/1Ts19mUZI7hKU4Z8GruMWy8le5DDZEgQ4/view
  • https://www.bilibili.com/video/BV1v94y1S727
  • https://www.jianshu.com/p/8f4f58b4b8ab