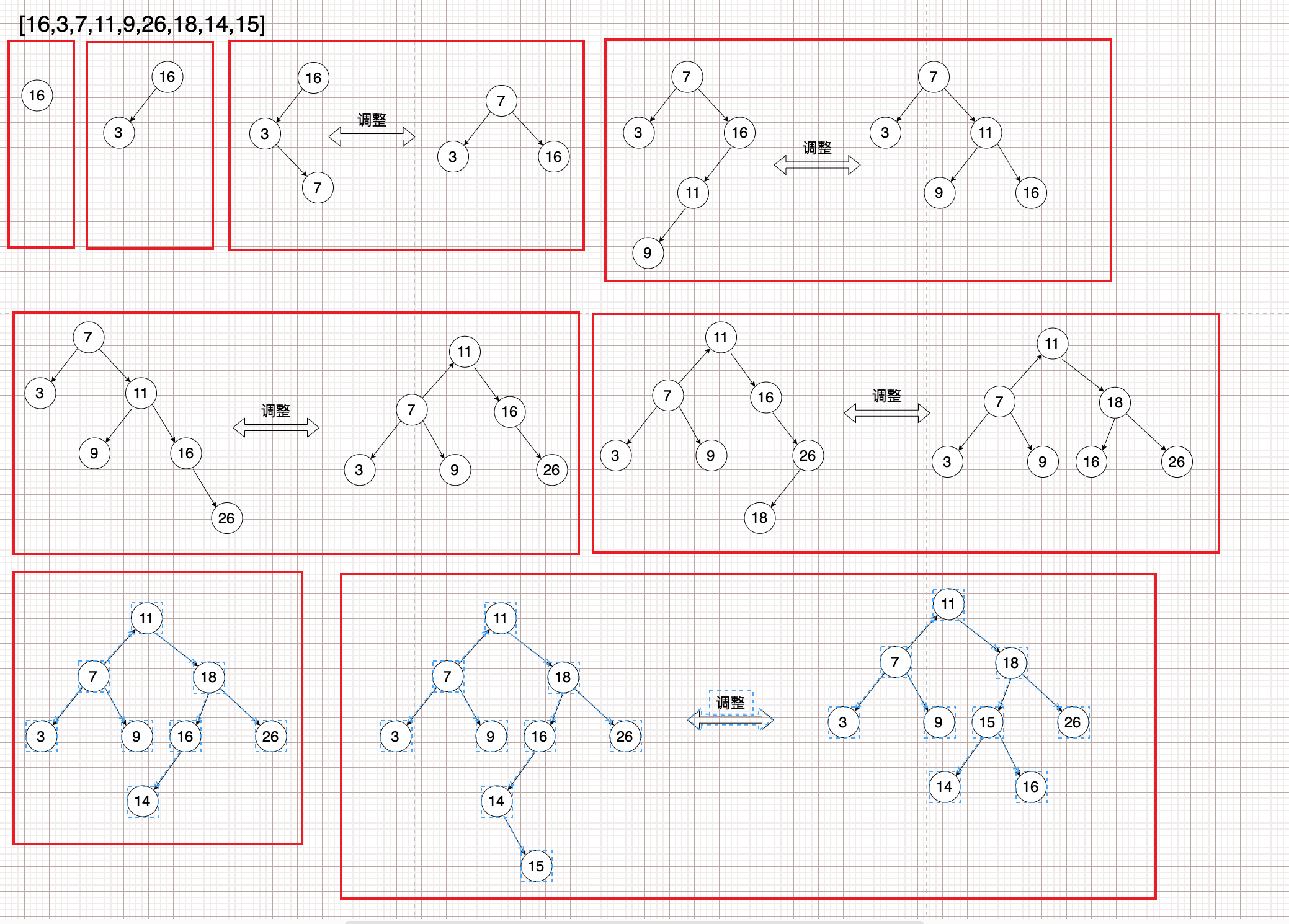
03-01-AVL-TREE

FGJ: Create:2024/02/24 Update: (2024-10-24)

Intro(AVL) #
平衡二叉树又称AVL树。它可以是一颗空树，或者具有以下性质的二叉排序树：它的左子树和右子树的高度之差(平衡因子)的绝对值不超过1且它的左子树和右子树都是一颗平衡二叉树。因此它也被称为高度平衡树。
查找、插入和删除在平均和最坏情况下的时间复杂度都是 \({\color{red}O(\log_2 N)}\)。增加和删除元素的操作则可能需要借由一次或多次树旋转，以实现树的重新平衡。
AVL 树得名于它的发明者 G. M. Adelson-Velsky 和 Evgenii Landis，他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。
- 来源 #
  为什么需要AVL：二叉搜索树一定程度上可以提高搜索效率，但是当原序列有序时，例如序列 A = {1，2，3，4，5，6}，构造二叉搜索树如下图。依据此序列构造的二叉搜索树为右斜树，同时二叉树退化成单链表，搜索效率降低为 \({\color{red}O(N)}\)。
  
  在此二叉搜索树中查找元素 6 需要查找 6 次。
  二叉搜索树的查找效率取决于树的高度，因此保持树的高度最小，即可保证树的查找效率。同样的序列 A，将其改为图右的方式存储，查找元素 6 时只需比较 3 次，查找效率提升一倍。
  可以看出当节点数目一定，保持树的左右两端保持平衡，树的查找效率最高。这种左右子树的高度相差不超过 1 的树为平衡二叉树。
- 定义 #
  简称平衡二叉树。由前苏联的数学家 Adelse-Velskil 和 Landis 在 1962 年提出的高度平衡的二叉树，根据科学家的英文名也称为 AVL 树
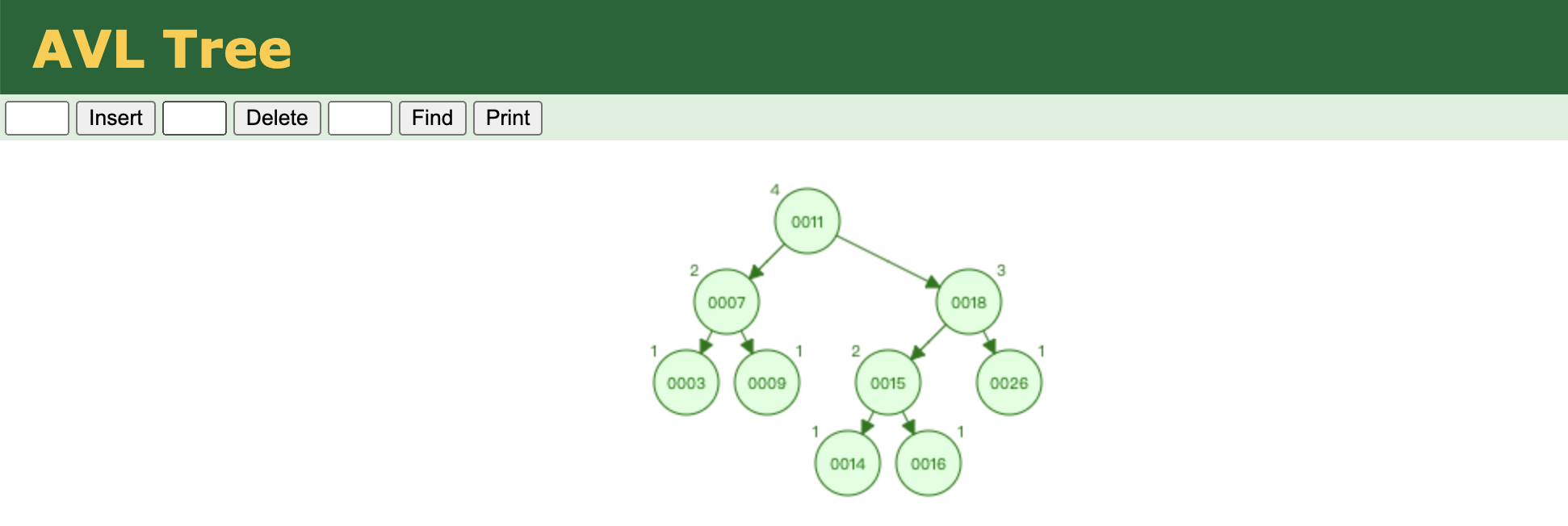
  示例AVL.
  反示例AVL.
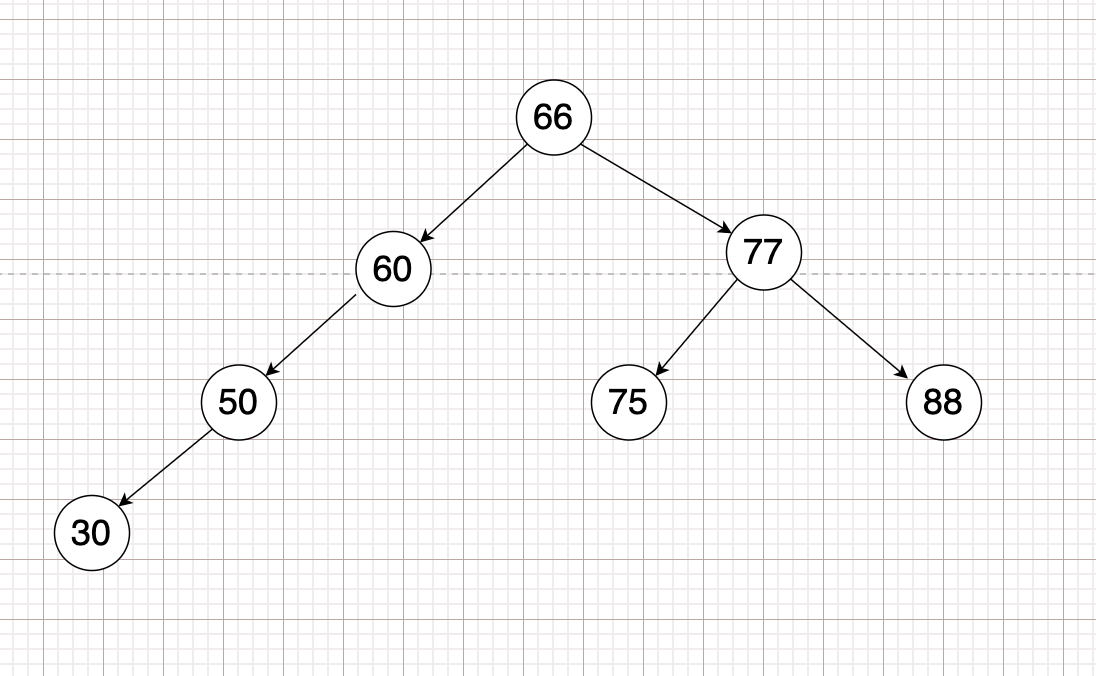
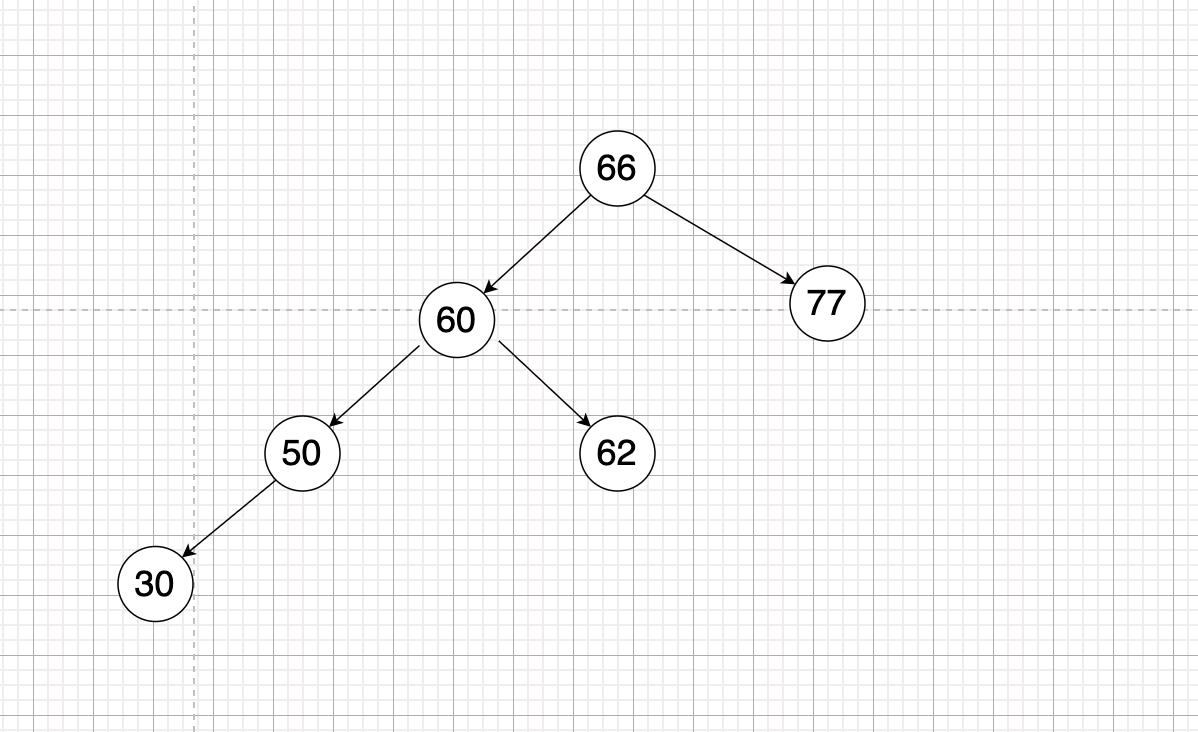
- 性质 #
  1. 可以是空树。
  2. 假如不是空树，任何一个结点的左子树与右子树都是平衡二叉树，并且高度之差的绝对值不超过 1。
- 平衡因子 #
  某节点的左子树与右子树的高度(深度)差即为该节点的平衡因子（BF,Balance Factor），平衡二叉树中不存在平衡因子大于 1 的节点。在一棵平衡二叉树中，节点的平衡因子只能取 0 、1 或者 -1 ，分别对应着左右子树等高，左子树比较高，右子树比较高。
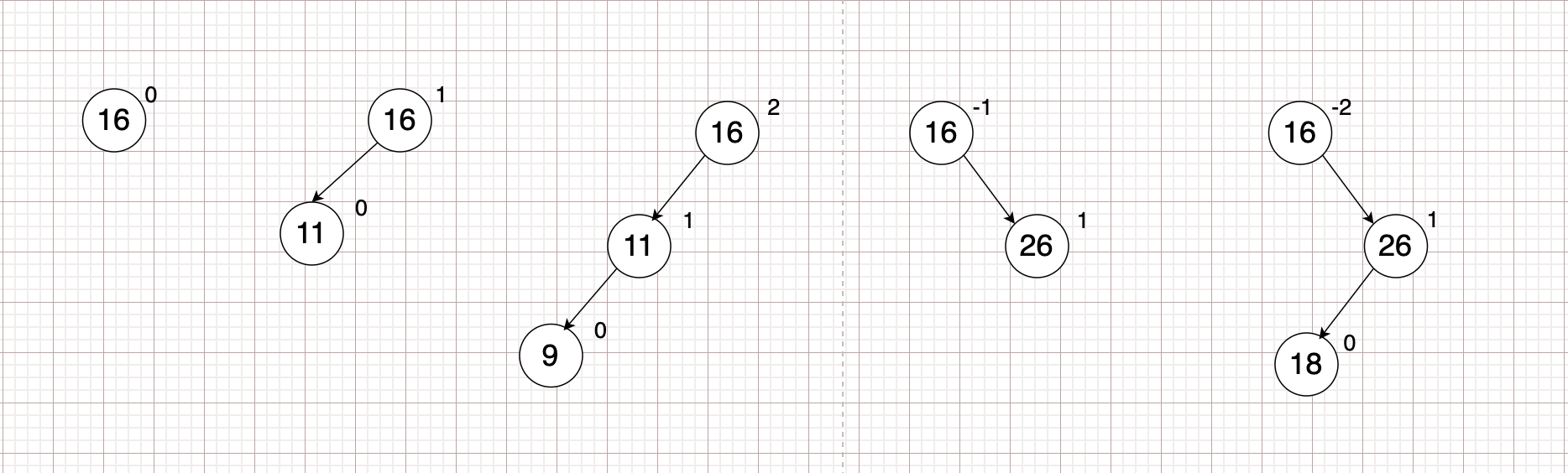
- 平衡 #
  - 解释 #
    平衡调整的步骤：
    1. 找平衡因子=2；
    2. 找插入新节点后失去平衡的最小子树；
    3. 平衡调整。
    
    要求：
    a. 距离插入节点最近
    b. 平衡因子绝对值大于1的节点作为根
  - 四种平衡方式 #
  - 样例 #
    以关键字序列[16,3,7,11,9,26,18,14,15]构造一棵AVL树(平衡二叉树)。
    验证