📓 Archive

TREE

FGJ: Create:2024/02/22 Update: (2024-10-24)

  • Intro(Tree) #

    • 一、什么是树？ #

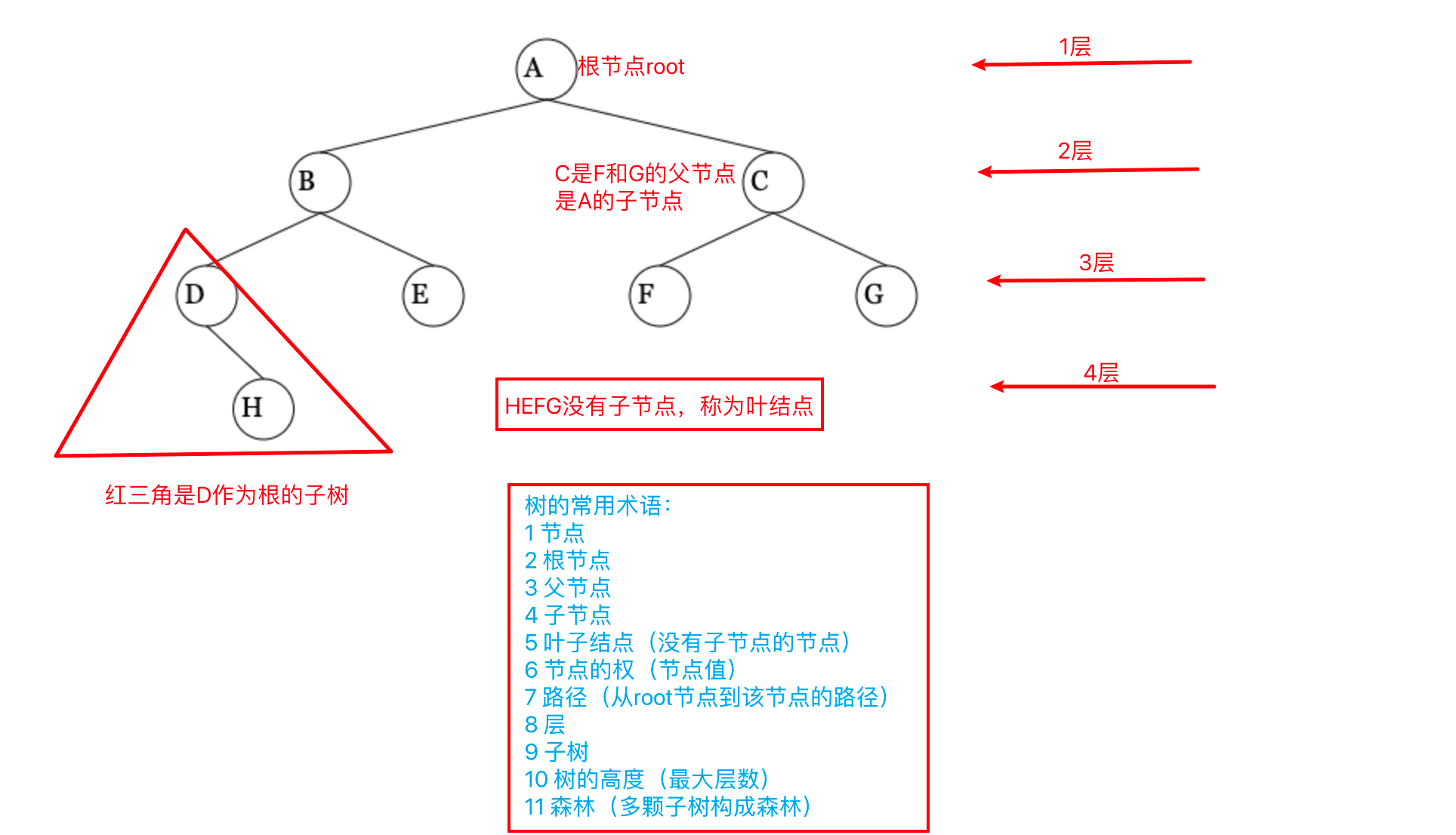
      在计算机科学中，树是一种非线性的数据结构，用于模拟具有层次关系的数据集合。它由有限节点组成，每个节点可以有零个或多个子节点。树的根节点是层次结构的顶部，其他节点都是其子节点。根据节点的度数（即子节点的数量），树可以分为二叉树、三叉树、多叉树等。

    • 二、树的遍历方式 #

      1. 先序遍历：先访问根节点，然后访问左子树，最后访问右子树。
      2. 中序遍历：先访问左子树，然后访问根节点，最后访问右子树。
      3. 后序遍历：先访问左子树，然后访问右子树，最后访问根节点。

    • 三、常见的树 #

      1. 二叉树：二叉树是树的一种特殊形式，每个节点最多有两个子节点（通常称为左子节点和右子节点）。二叉树的遍历方式有限，通常是先序遍历、中序遍历和后序遍历。
      2. 二叉查找树：二叉查找树是一种特殊的二叉树，它的每个节点的左子节点的值小于或等于它的值，而右子节点的值大于或等于它的值。这种结构使得在查找、插入和删除元素时具有高效的性能。
      3. 平衡二叉树：平衡二叉树是一种特殊的二叉树，它的左右子树的深度差不超过1，并且每个节点的左子树和右子树的深度都接近于整个树的深度。平衡二叉树的插入、删除等操作的时间复杂度较低，为 \(O(logN)\)。
        • AVL树：AVL树是一种自平衡的二叉查找树，它通过旋转操作保持平衡状态。AVL树的插入、删除等操作的时间复杂度为 \(O(logN)\)。
        • 红黑树：红黑树是一种自平衡的二叉查找树，它通过颜色和旋转操作保持平衡状态。红黑树的插入、删除等操作的时间复杂度为 \(O(logN)\)。
      4. 2-3树
      5. B树：B-tree是一种平衡的多叉查找树，它可以用于磁盘文件系统、数据库索引等场合。B-tree的每个节点可以有多个子节点，并且每个节点的值域大小有限制。B-tree的插入、删除等操作的时间复杂度为 \(O(logN)\)。
      6. B+树
      7. B*树

Demo #

graph TB 1((1))---21((2))---31((3))---41((4)) 21--- n((null)) 31--- n1((null)) 1((1))---22((5))---n2((null)) 22---32((6))

Reference #

comments powered by Disqus